Funcions inverses
La funció que fa l’efecte contrari al que fa una altra funció n’és la funció inversa. Per exemple, la funció inversa de la funció elevar al cub, \(f(x)=x^3\) és la funció arrel cúbica, perquè el contrari del cub és l’arrel cúbica, de manera que si primer elevem un nombre al cub i després en fem l’arrel cúbica recuperarem el valor inicial: \(8 \underbrace{\longrightarrow}_{8^3} 512 \underbrace{\longrightarrow}_{\sqrt[3]{512}} 8,\space \text{és a dir, que \( \sqrt[3]{8^3} = 8 \)} \). I passa el mateix si primer extraem l’arrel cúbica i després en fem el cub, \(8 \underbrace{\longrightarrow}_{\sqrt[3] 8} 2 \underbrace{\longrightarrow}_{2^3} 8, \space \text{és a dir, que \( \sqrt[3]8^3 = 8\)} \).
La funció inversa de la funció \(f(x)\) es representa com \(f^{-1}(x)\). En el nostre exemple, si \(f(x)=x^3\) la inversa és \(f^{-1}(x)=\sqrt[3]x\).
No deuria costar-vos massa entendre que la inversa de \(f(x)=x+4\) és \(f^{-1}(x)=x-4\) o que la inversa de \(f(x)=x/4\) és \(f^{-1}(x)=4x\). Però potser us trobareu una sorpresa si mireu de trobar la funció inversa de \(f(x)=1/x\).
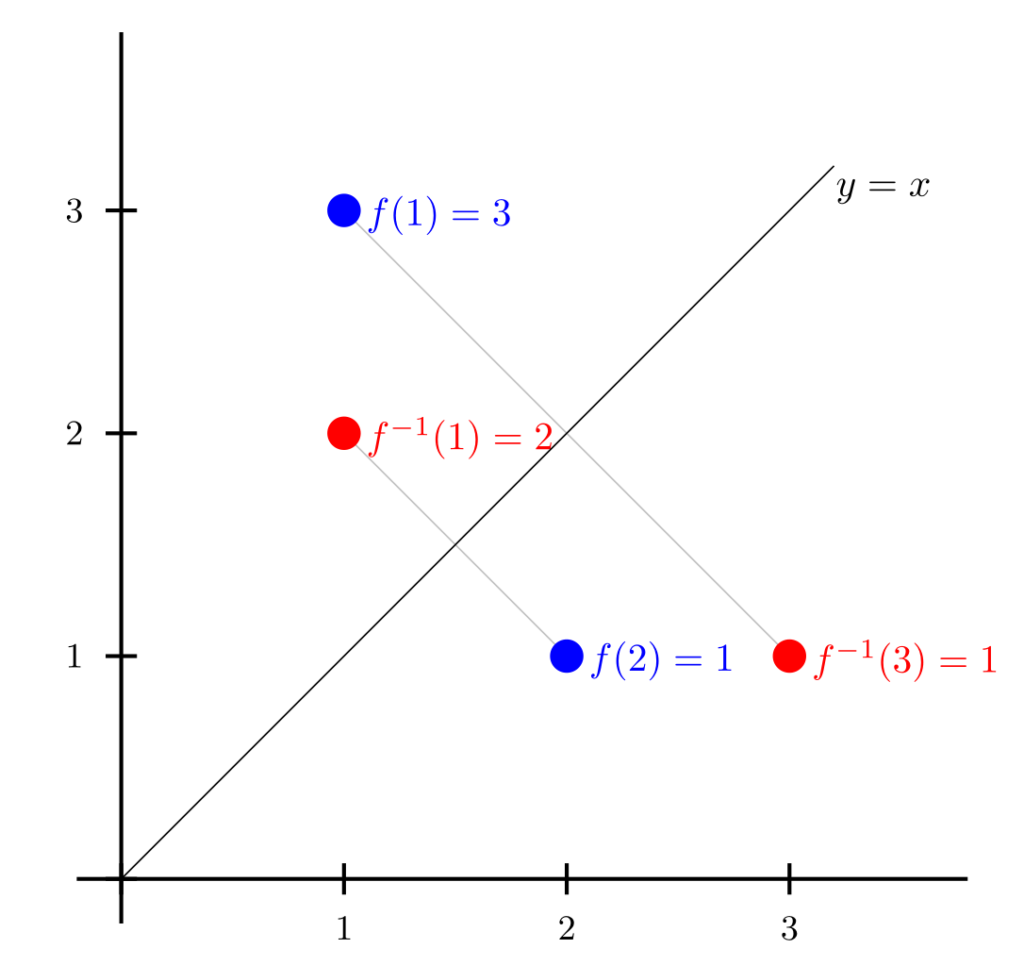
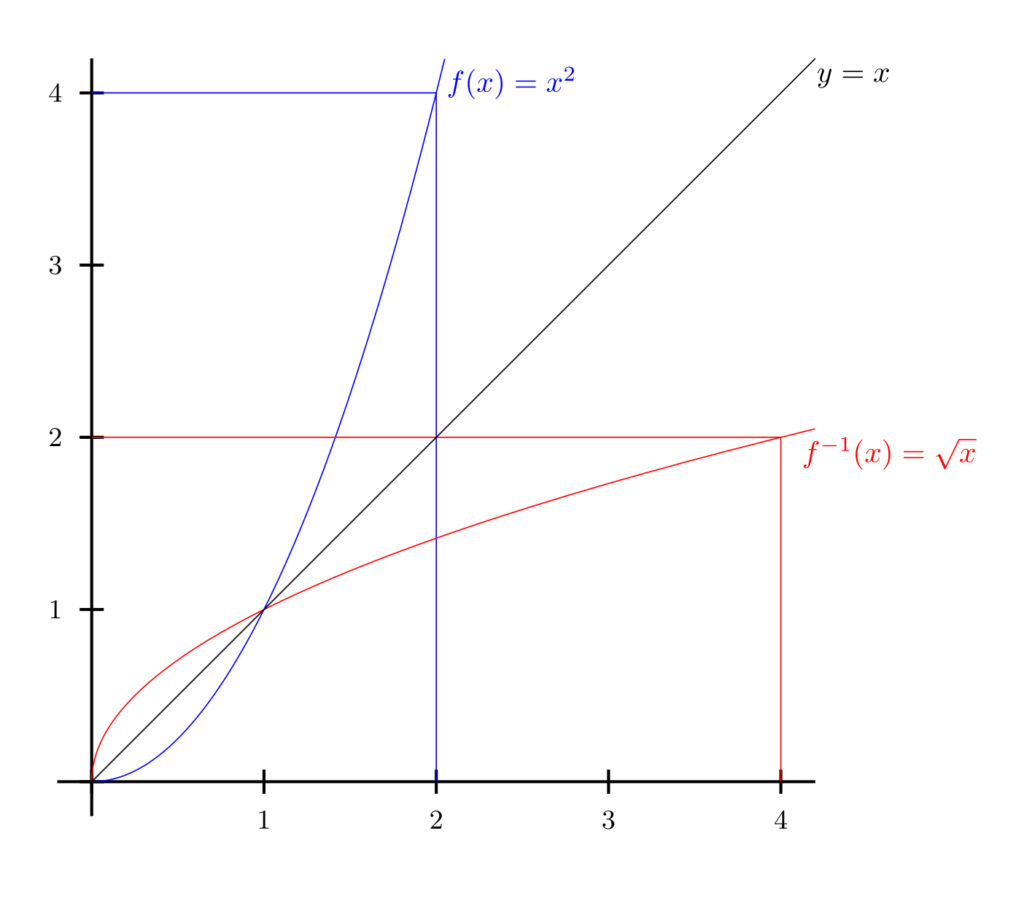
Si dibuixem la gràfica d’una funció \(f(x)\) i la de la funció inversa \(f^{-1}(x)\) trobarem que hi ha una simetria respecte a la recta \(y=x\), perquè fer la inversa és equivalent a intercanviar els papers dels dos eixos coordenats: si la funció \(f(x)\) transforma el nombre \(2\) en \(1\), la inversa \(f^{-1}(x)\) transformarà \(1\) en \(2\) (i els punts de coordenades \((2,1)\) i \((1,2)\) són simètrics respecte a la recta \(y=x\)); o, si \(f(x)\) transforma el nombre \(1\) en \(3\), la inversa \(f^{-1}(x)\) transformarà \(3\) en \(1\).
Les funcions logarítmiques
A la inversa de la funció exponencial l’anomenem funció logarítmica. O, més ben dit, la inversa de l’exponencial de base \(a\), \(\exp_ax\), és la funció logarítmica de base \(a\), \(\log_ax\).
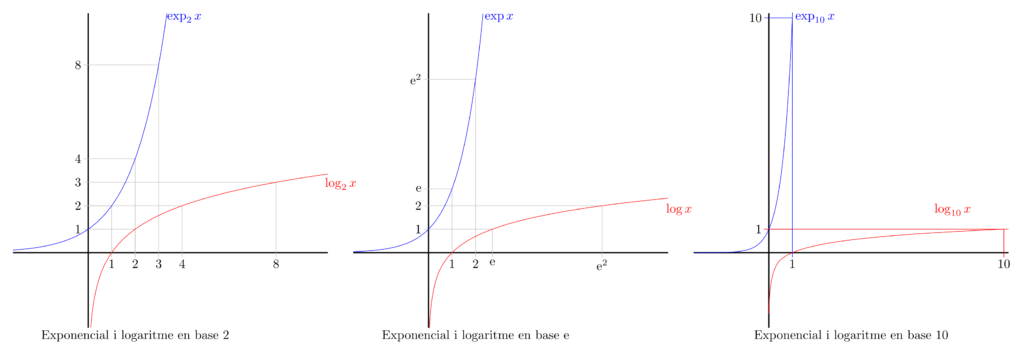
Quan la base és el nombre \(e\), en comptes de \(\log_ex\) escrivim simplement \(\log x\). Fem això perquè, com ja hem dit abans, els matemàtics són (som) bojos i creiem que l’única base decent per als logaritmes és el nombre \(e\). Però a una persona normal, segurament li semblaran més raonables els logaritmes en base \(10\), que són els que s’han utilitzat tradicionalment en les aplicacions pràctiques; d’altra banda, en el camp de la informàtica també és freqüent l’ús dels logaritmes en base \(2\).
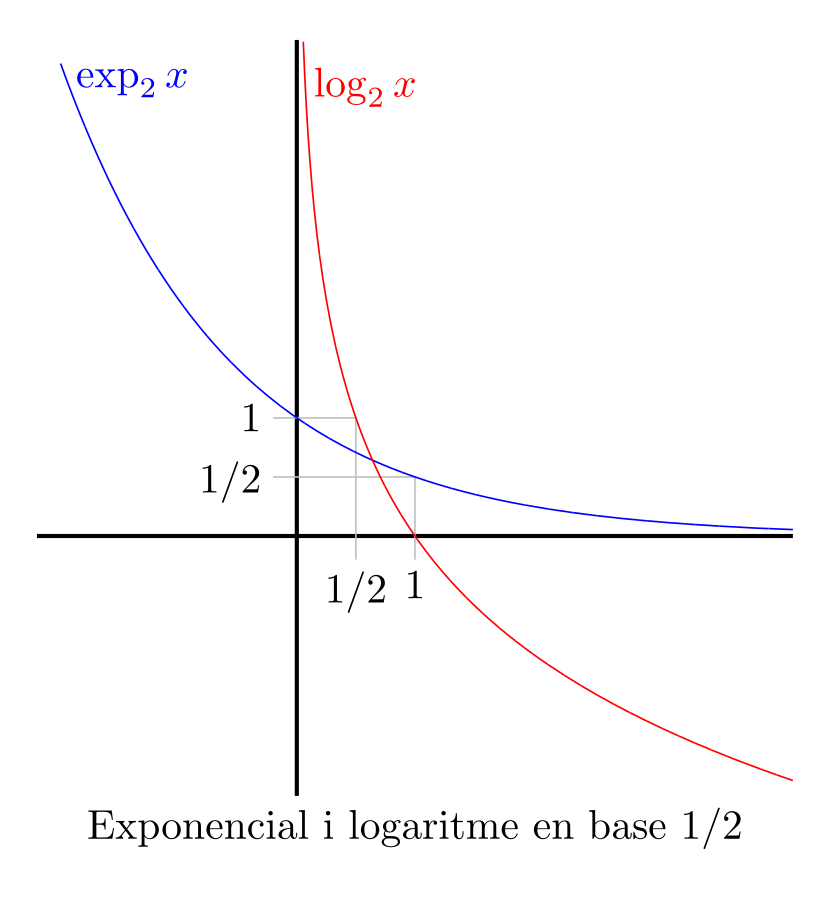
En qualsevol cas, com que \(\exp_a x=a^x\) és clar (com es veu als gràfics) que com més gran és \(a\) més de pressa creix l’exponencial i per tant, més lentament creix el logaritme. D’altra banda, si \(a<1\) les funcions exponencial i logarítmica són decreixents (a la figura de la dreta es mostren l’exponencial i el logaritme en base \(1/2\)).
De cada propietat de les potències se’n dedueix una dels logaritmes:
Propietats de les potències (o de la funció exponencial)
- \(\exp_a 0=1\)
- \(\exp_a(x_1+x_2)=\exp_a{x_1}\exp_a{x_2}\)
- \(\exp_a{\left(x_1-x_2\right)}=\frac{\exp_a{x_1}}{\exp_a{x_2}}\)
- \(\exp_a (nx)=\left(\exp_a x\right)^n\)
Propietats dels logaritmes (o de la funció logarítmica)
- \(\log_a 1=0\)
- \(\log_a(x_1x_2)=\log_a x_1+\log_a x_2\)
- \(\log_a\left(\frac{x_1}{x_2}\right)=\log_a x_1-\log_a x_2\)
- \(\log_a x^n=n\log_a x\)
Recordareu que al capítol anterior vam dir que \(\frac12=\mathrm e^{-\log 2}\). Això, ara, és clar, perquè \(\mathrm e^{-\log 2}=\mathrm e^{0-\log 2}=\mathrm e^{\log 1-\log 2}=\mathrm e^{\log\left(\frac12\right)}=\frac12\).
Problemes inversos
Els problemes inversos es resolen (lògicament) fent servir les funcions inverses. Per exemple, al final del capítol anterior déiem que, per saber quina és l’antiguitat d’una mostra fent servir la prova del carboni 14, sabent que la proporció actual de \(^{14}C\) és \(x\) el que cal és que decidim quant val \(t\) si \(x=x_0\exp \left(-\left(\log 2\right)\frac{t}{T}\right)\)? Cal que aïllem la lletra \(t\), que apareix al costat dret d’aquesta igualtat. I això ja ho podem fer, perquè coneixem els logaritmes:\[x=x_0\exp \left(-\left(\log 2\right)\frac{t}{T}\right) \Longleftrightarrow \frac{x}{x_0}=\exp \left(-\left(\log 2\right)\frac{t}{T}\right)\]I, com que el logaritme és la funció inversa de l’exponencial, sabem que \(\frac{x}{x_0}=\exp\left(\log\left(\frac{x}{x_0}\right)\right)\), així que podem substituir: \[\exp\left(\log\left(\frac{x}{x_0}\right)\right)=\exp \left(-\left(\log 2\right)\frac{t}{T}\right)\]
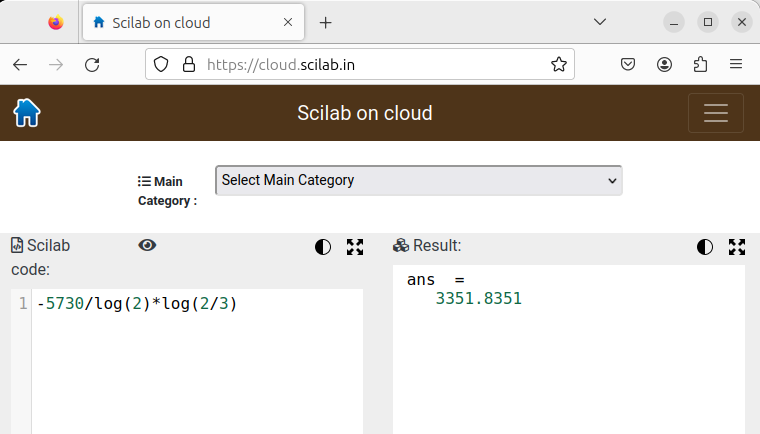
I d’ací es dedueix que \( \log\left(\frac{x}{x_0}\right)=-\left(\log 2\right)\frac{t}{T}\). I ara ja és molt fàcil aïllar la \(t\):\[t=-\frac{T}{\log 2}\log\left(\frac{x}{x_0}\right)\quad\text{(on \(T\) és la semivida del carboni 14, }T=5730\text{ anys)}\]Per exemple, si la proporció actual és de \(x=0{,}8\cdot 10^{-12}\) àtoms de carboni 14 per cada àtom de carboni 12 (en comptes dels \(x_0=1{,}2\cdot 10^{-12}\) àtoms de carboni 14 per cada àtom de carboni 12 inicials), la mostra té uns \[t=-\frac{5730}{\log 2}\log\left(\frac{0{,}8\cdot 10^{-12}}{1{,}2\cdot 10^{-12}}\right)t=-\frac{5730}{\log 2}\log\left(\frac{2}{3}\right)\approx 3352\text{ anys.}\](els càlculs podeu fer-los fàcilment amb qualsevol calculadora científica; per exemple, en https://cloud.scilab.in)
Els deures
Exercici 1: Suposem que fa tres anys i mig vàrem dipositar al banc la quantitat de 10.000€ i que en l’actualitat el nostre capital és de 15.219,62€. Si el banc ha aplicat la fórmula de l’interès continu, quin tipus d’interès ens ha aplicat? (No és gaire probable que aquest banc existisca)