Al capítol tercer hem vist que si invertim \(C_0\) euros a un interès continu del \(R\%\) anual durant \(n\) anys el capital final serà de \(C_n=C_0e^{nr}\) euros.
La funció exponencial
En aquesta fórmula no és necessari que \(n\) siga un nombre exacte d’anys: és vàlida igualment si \(n\) és un nombre enter (un any, dos anys o vint-i-cinc anys) com si l’apliquem a dos anys i mig (\(n=2{,5}=5/2\)) a dos anys i tres mesos (\(n=2{,}25=9/4\)) o a 3 anys, 51 dies, 16 hores, 21 minuts i 5 segons (\(3,1415926\) anys).
Als matemàtics ens agrada fer servir la lletra \(n\) per representar un nombre enter, però per als nombres reals ens fa més gràcia la lletra \(x\), així que la fórmula de l’interès continu la entenem com una funció, que a cada nombre \(x\) li associa el valor \(C_0 e^{rx}\). Quan \(C_0=1\) i \(r=1\), aquesta és la funció exponencial:
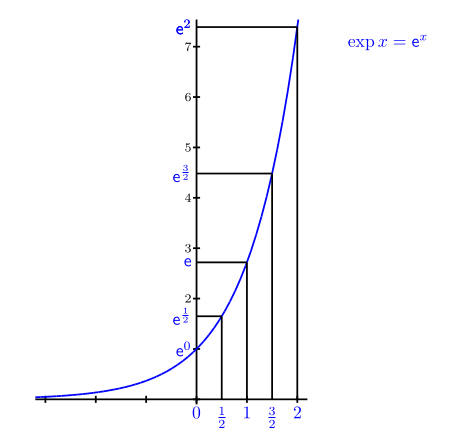
\[ \fbox{\(\exp x = e^x\)}\]
Ben mirat, hauríem de parlar de la funció exponencial de base \(e\), perquè també hi ha la funció exponencial de base \(2\), \(\exp_2 x=2^x\), la de base \(10\), \(\exp_{10} x=10^x\), i, en general, si \(a\) és un nombre positiu, la de base \(a\), \(\exp_a x=a^x\). Així que, segurament, hauríem d’escriure \(\exp_e x\) quan la base és \(e\); però com que els matemàtics som bojos i creiem que l’única funció exponencial important és la de base \(e\), la representem simplement com \(\exp x\): hi ha moltes funcions exponencials, però només una és la funció exponencial.
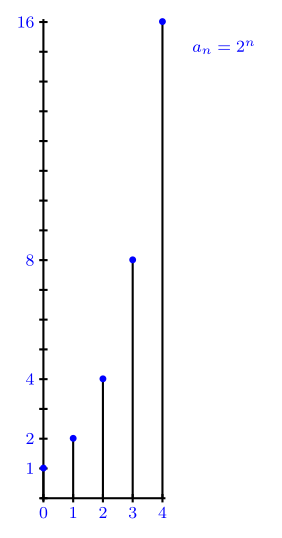
Quan les variables són només nombres enters no negatius (\(0,1,2,3,\dots\)) la funció exponencial de base \(r\) és el que coneixem com a progressió geomètrica de raó \(r\): \(1,r,r^2,r^3,\dots\)
La funció exponencial creix molt ràpidament (per això sentim molt sovint que un determinat creixement és exponencial (o geomètric), encara que això no sempre és estrictament cert). Això és degut al fet que\[\exp (x+y)=\mathsf e^{x+y}=\mathsf e^{x}\mathsf e^{y}=\exp x \cdot \exp y\] és a dir, que aquesta funció transforma sumes en multiplicacions; per exemple, quan la variable es duplica la funció s’eleva al quadrat: \(\exp 3 \approx 20{,}085537\), \(\exp 6 \approx 403{,}42879\)
Les funcions exponencials de base natural i els sistemes de numeració
El sistema de numeració decimal, que conscientment o inconscientment tots fem servir, és, ben mirat, una aplicació de la funció \(\exp_{10}\), perquè quan escrivim, per exemple, \(a=1.234\) el que estem fent és representar el nombre \begin{align*}a&=1000+200+30+4\\&=1\cdot 10^3+2\cdot 10^2+3\cdot 10^1+4\cdot 10^0\end{align*} De fet, la influència de les potències de \(10\) en la nostra concepció dels nombres és tan gran que, fins i tot, quan diem «mil dos-cents trenta-quatre», estem dient «deu al cub més dos per deu al quadrat més tres per deu més quatre».
El sistema de numeració posicional és un dels grans invents de la humanitat. A l’antiga Roma escrivien \(\mathrm{MCCXXXIV}\) (o \(\mathrm{MCCXXXIIII}\) ?), en comptes de \(1234\), així que, si mai volien escriure el resultat d’una multiplicació, en lloc de\[1234\times3=3702\]haurien d’escriure (si ens refiem del traductor del Google)\[\mathrm{MCCXXXIV} \text{ vicibus } \mathrm{III} \text{ sunt pares } \mathrm{MMMDCCII}\](al marge del fet que l’algorisme de la multiplicació, tal com ens el van explicar de menuts, seria absolutament impracticable).
El nostre sistema de numeració és decimal perquè fa servir només deu símbols (\(0,1,2,\dots,9\)) i posicional, perquè el valor de cada símbol depén de la seua posició: el \(4\) en el nombre \(1234\) val quatre, però el \(2\) val dos-cents. Això ens permet escriure qualsevol nombre (si més no natural), per gran que siga: \(1234\) vol dir \(1\cdot 10^3+2\cdot 10^2+3\cdot 10^1+4\cdot 10^0\).
Diuen que fem servir el sistema decimal perquè a les mans tenim deu dits (i allò natural és comptar amb els dits). Però en alguns moments del passat (i encara en les divisions del temps en hores, minuts i segons) hem utilitzat les bases seixanta o dotze. El cas és que podem fer servir qualsevol nombre de símbols bàsics per a representar els nombres: per exemple, amb tres símbols, com ara, \(0,1,2\), tenim el sistema ternari, en el qual, el nombre set s’escriu \(21\) (perquè dos \(\times\) tres \(+\) u \(=\) set). Pot semblar absurd (o molt estrany) que \(21\) siga set, en comptes de vint-i-u, però això només és perquè tenim profundament assumit el sistema decimal.

Les màquines tenen molta més memòria que no nosaltres, però són (o eren) bastant ximpletes i només entenen (entenien) allò que és perfectament lògic: si/no, encès/apagat, 0/1, així que fan servir el sistema de numeració binari: només dos símbols: \(0,1\).
Però els individus que parlen amb les màquines (coneguts com a informàtics) són en realitat humans, així que els costa molt d’entendre un nombre escrit amb una llarga llista d’uns i zeros i, per això, fan servir el sistema de numeració en base hexadecimal (setze símbols: \(0,1,2,\dots,9,A,B,C,D,E,F\)), perquè \(16\) és una potència de dos i resulta més o menys senzill de traduir entre les bases dos i setze\[\begin{array}{ccccccccc} \text{Decimal} & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 &11 & 12 & 13 & 14 & 15 & 16 & 17 \dots\\\hline \textrm{Binari} & 0 & 1 & 10 & 11 & 100 & 101 & 110 & 111 & 1000 &1001 & 1010 & 1011 & 1100 & 1101 & 1110 & 1111 & 10000 & 10001 \\\hline \textrm{Hexadecimal} & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & A & B & C & D & E & F & 10 & 11\end{array}\] En el sistema decimal, les potències de deu (u, deu, cent, mil, deu-mil…) s’escriuen amb un u i diversos zeros: \(1,10,100,1000,10000\dots\) En base dos, això passa amb les potències de dos: \(1,10,100,1000,10000\dots\) vol dir u, dos, quatre, vuit, setze… En base setze, \(1,10,100\dots\) és u, setze, dos-cents cinquanta-sis…
La història de l’inventor dels escacs i els grans de blat
De segur que ja la coneixeu: diuen que el califa, meravellat pel joc que aquell home havia inventat li va dir que li donaria allò que li demanés, a la qual cosa l’inventor li respongué que volia un gra de blat pel primer escac del tauler, dos grans pel segon, quatre pel tercer, vuit pel quart i així, sempre doblant el nombre de grans, fins arribar a l’últim escac. El comanador dels creients es queda sorprès de que aquell home es conformara amb tan poca cosa… però aquell home sabia matemàtiques, així que igual no demanava tan poc com creia el califa. Quants grans de blat li estava demanant l’inventor?
Es tracta d’una progressió geomètrica, \(1,2,2^2,2^3,\dots,2^{63}\) que cal sumar: el nombre total de grans és la suma \(S=1+2+2^2+2^3+\dots+2^{63}\). Segurament us van ensenyar la fórmula per calcular aquesta suma i, probablement, l’haureu oblidada. Però no us preocupeu, perquè farem la suma sense recordar aquella fórmula:
Si la suma \(S=1+2+2^2+2^3+\dots+2^{63}\) la multipliquem per \(2\) obtindrem que \(2S=2+2^2+2^3+\dots+2^{63}+2^{64}\) i si ara restem \(2S-S\) resultarà que \begin{align*}S=2S-S={}&\phantom{-1-{}}{\not2}+{\not2^2}+{\not2^3}+\dots+{\not2^{63}}+2^{64}\\&-1-{\not2}-{\not2^2}-{\not2^3}-\dots-{\not2^{63}}\\={}&2^{64}-1\end{align*}
El califa ha de donar-li, a l’inventor dels escacs, \(2^{64}-1\) grans de blat: poca cosa, més de 1100 anys de la producció mundial de blat de tot el món (podeu veure aquesta aproximació en aquest altre post). Però el que m’interessa remarcar ací és que el nombre total de grans de blat es calcula molt fàcilment si en comptes de la base 10 fem servir la base 2: La suma que cal calcular és
\begin{align*} 1&\\10&\\100&\\\vdots&\\\vdots&\\\vdots&\\10000000000000000000000000000000000000000000000000000000000000&\\100000000000000000000000000000000000000000000000000000000000000&\\1000000000000000000000000000000000000000000000000000000000000000&\space (63 \text{ zeros})\\\hline1111111111111111111111111111111111111111111111111111111111111111&\space (64 \text{ uns})\end{align*}
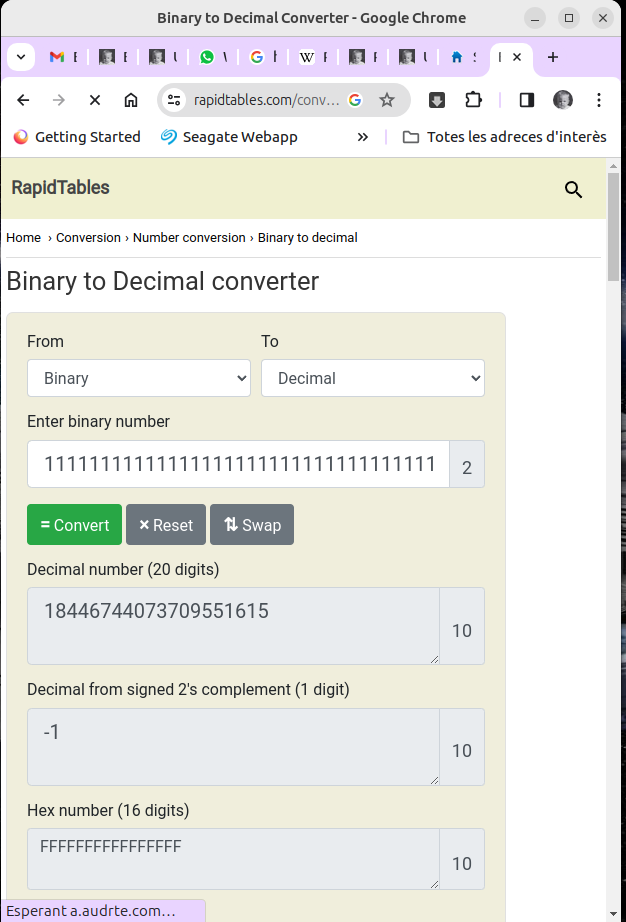
Com que a la xarxa es troba de tot, a https://www.rapidtables.com/convert/number/binary-to-decimal.html hi ha un conversor de binari a decimal que ens permet passar a la notació decimal aquest nombre: \(2^{64}-1=18_3446.744_2073.709_1551.615\) (ço és, uns 18 trilions i mig de grans de blat).
Els deures
Exercici 1: Demostreu que el nombre total de grans de blat, en base setze és \(FFFFFFFFFFFFFFFF\) (setze efes). Suggeriment: \(2^{64}-1=16^{16}-1\)