El nombre \(e\) és un altre gran protagonista de les matemàtiques. El trobem, com veurem en aquest capítol, en estudiar l’interès compost. Però també és la base dels logaritmes naturals i és ben important en el càlcul diferencial i integral, en l’expressió polar dels nombres complexos (que és el que ens interessa per justificar la fórmula d’Euler)…
Interès simple, interès compost… interès continu
Abans, quan els banquers no ens cobraven per fer servir els nostres diners per als seus negocis, sinó que ens pagaven per fer-ho, una opció interessant per traure profit dels nostres estalvis era dipositar-los al banc a canvi d’un interès: jo deixe uns diners al banc i aquest me’ls remunera (per exemple) a un interès del 10% anual.
Interès simple
Això vol dir que d’ací a un any el capital inicial, diguem \(C_0\), produirà un interès de \(\frac{10}{100}C_0=0{,}1C_0\) i el capital final serà \(C_1=C_0+0{,}1C_0=1{,}1C_0\). De manera més general, si l’interès és del \(R\%\), \(C_1=\left(1+\frac{R}{100}\right)C_0\). Per simplificar escriurem \(r=R/100\): \(C_1=\left(1+r\right)C_0\). \(rC_0\) és el que es coneix popularment com el rèdit: teníem \(C_0\) euros i hem acoseguit un rèdit de \(rC_0\) euros.
Ara bé, si hem pactat amb el banc que el diposit el fem per un període de \(10\) anys, guanyarem \(10rC_0=C_0\) i el nostre capital arribarà a \(C_{10}=\left(1+10r\right)C_0\) (si l’interès és del \(10\%\) anual, en deu anys duplicarem el capital, perquè tindrem \(C_{10}\left(1+10\frac{10}{100}\right)C_0=2C_0\)).
Això és el que s’anomena capitalització amb interès simple.
La fórmula de l’interès simple és \[C_n=(1+nr) C_0\]
\(C_0\) és el capital inicial, \(r=R/100\) (l’interès anual és \(R\%\)) i \(n\) el nombre d’anys transcorreguts.
Interès compost
L’alternativa (molt més freqüent i justa) és l’interès compost: si durant el primer any guanyem \(rC_0\) i el nostre capital ha passat a ser \(C_1=\left(1+r\right)C_0\) així que aquesta és la base sobre la qual calcularem els interessos del segon any, de manera que el capital, al cap de dos anys serà \(C_2=\left(1+r\right)C_1=\left(1+r\right)\big(\left(1+r\right)C_0\big)=\left(1+r\right)^2C_0\). En 10 anys, \(C_{10}=\left(1+r\right)^{10}C_0\). Si l’interès és del \(10\%\) anual, en deu anys tindrem \(C_{10}=\left(1+\frac{1}{10}\right)^{10}C_0\). Fent servir la calculadora, \(\left(1+\frac{1}{10}\right)^{10}\approx 2{,}5937425\), així que \(C_{10}\approx2{,}5937425 C_0\) (no hem multiplicat per \(2\) sinó per quasi \(2{,}6\) el capital inicial).
Però un any és molt de temps. Perquè ens hem de conformar amb actualitzacions anuals del capital? Per què no ho fem cada mes? El client pot argumentar que si l’interès en un any és \(r\), en un mes ha serà \(r/12\), així que, al cap d’un mes el capital s’ha d’actualitzar a \(C_{1}=\left(1+\frac{r}{12}\right)C_0\), el segon mes, \(C_{2}=\left(1+\frac{r}{12}\right)C_{1}=\left(1+\frac{r}{12}\right)^2C_{0}\), a l’any, \(C_{12}=\left(1+\frac{r}{12}\right)^{12}C_{0}\) i, als \(10\) anys (\(120\) mesos), \(C_{120}=\left(1+\frac{r}{12}\right)^{120}C_{0}\). Per tant, si l’interès és del \(10\%\) anual i les capitalitzacions de l’interès són mensuals, \(C_{120}=\left(1+\frac{10/100}{12}\right)^{120}C_{0}=\left(1+\frac{1}{120}\right)^{120}C_{0}\). Una nova consulta a la calculadora ens dona que \(\left(1+\frac{1}{120}\right)^{120}\approx 2{,}7070415\), així que \(C_{120}\approx 2{,}7070415C_0\) i, capitalitzant mes a mes, en \(10\) anys ja multipliquem el capital per una mica més de \(2{,}7\).
Això ens pot fer pensar que, com més menut siga el període de capitalització, més gran serà el nostre guany i que fent-lo infinitament petit aconseguirem un guany infinit! En realitat, és cert que el guany és més gran com més menut és el període de capitalització, però el guany no és infinit, com veurem tot seguit:
Fem números suposant que fem les actualitzacions diàriament: deu anys són 3650 dies (bé, en realitat dos o tres més, per allò dels anys de traspàs) així que en deu anys al \(10\% \) tindrem \(C_{3650}=\left(1+\frac{10/100}{365}\right)^{3650}C_{0}=\left(1+\frac{1}{3650}\right)^{3650}C_{0}\approx2{,}7179096\).
Actualitzant cada hora o, millor encara, cada minut! tindríem \(C_{24\times3650}=\left(1+\frac{1}{24\times3650}\right)^{24\times3650}C_{0}\approx2{,}7182663C_0\) o \(C_{60\times24\times3650}=\left(1+\frac{1}{60\times24\times3650}\right)^{60\times24\times3650}C_{0}\approx2{,}7182816C_0\)
Així que, si l’interès és del \(10\%\) anual, en 10 anys el capital final és més gran com més petit és el període de capitalització, però ho fa cada vegada més lentament.
La fórmula de l’interès compost és \[C_{nm}=\left(1+\frac{r}{m}\right)^{nm} C_0\]
Ací, \(C_0\) és el capital inicial, \(r=R/100\) (l’interès anual és \(R\%\)), \(m\) és el nombre de períodes en què es divideix l’any i \(n\) el nombre d’anys transcorreguts.
En el cas d’un any al \(100\%\) anual, \(C_m=\left(1+\frac{1}{m}\right)^m C_0\).
En el nostre exemple, el que hem anat fent fins ara és calcular els valors de \((1+1/m)^m\) quan \(m\) és igual a \(1,10,120,3650,\dots\):
\[\begin{array}{ccccccc} m & 1 & 10 & 120 & 3650 & 87600 & 5256000 \\ (1+1/m)^m & 2 & 2{,}5937425 & 2{,}7070415 & 2{,}7179096 & 2{,}7182663 & 2{,}7182816 \end{array}\]
Interès continu
El problema, més o menys com l’estem plantejant ací, el va estudiar Jakob Bernoulli, que va notar que, en realitat, el guany no es fa infinit encara que el període de capitalització es faça infinitament menut.
La successió \((1+1/m)^m\) és creixent (com més gran és \(m\) més gran és la successió), però no creix fins l’infinit. En el límit (quan \(m\) es fa més i més gran), \((1+1/m)^m\) va creixent i acostant-se al nombre que es coneix com \(e\):
Definició: El nombre \(e\) és
\[e=\lim_{m\rightarrow \infty}\left(1+\frac{1}{m}\right)^{m} =2{,}7182818281459045\dots\]
Portant al límit l’interès compost, tindríem que un capital d’un euro, dipositat a un \(10\%\) d’interès anual durant deu anys (o dipositat a un \(100\%\) d’interès anual durant un any), si les actualitzacions de capital es feren instantàniament, es convertiria en \(e\) euros. Això és el que s’anomena interès continu. En general, un euro es converteix en \(\lim_{m\rightarrow \infty}\left(1+\frac{r}{m}\right)^{nm}\) euros i, fent servir les propietats dels límits, es pot provar que
\[ \lim_{m\rightarrow \infty}\left(1+\frac{r}{m}\right)^{nm} = \left(\lim_{m\rightarrow \infty}\left(1+\frac{1}{m/r}\right)^{m/r}\right)^{nr} = e^{nr}\]
Així que la fórmula de l’interès continu és \[C_{n}=e^{nr}C_0\]
On \(C_0\) és el capital inicial, \(r=R/100\) (l’interès anual és \(R\%\)) i \(n\) el temps transcorregut, mesurat en anys.
Un exemple
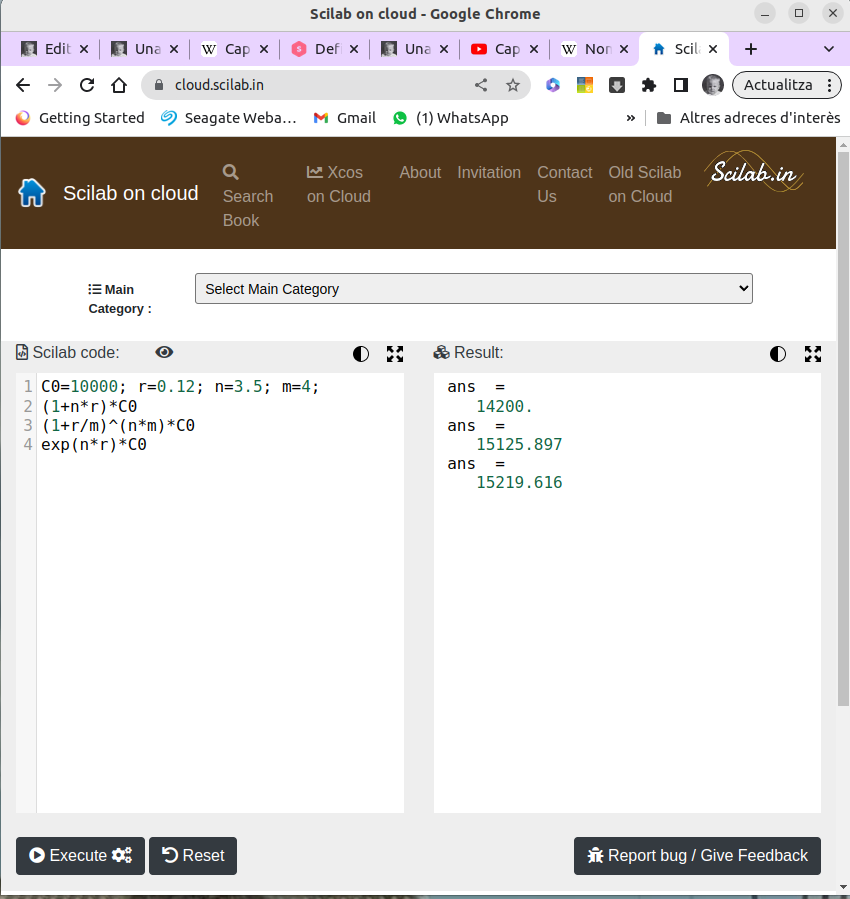
Quin serà el capital final, al cap de tres anys i mig, si dipositem un capital inicial de \(10.000€\) al \(12\%\) anual, en els casos de capitalització amb interès simple, amb interès compost amb actualitzacions trimestrals o amb interès continu?
Aplicant les fórmules corresponents obtenim
- Amb interès simple: \((1+0{,}12*3.5)10.000=14.200€\)
- Amb interès compost: \(\left(1+\frac{0{,}12}{4}\right)^{4\times3{,5}}=15.125{,}90€\)
- Amb interès continu: \(e^{3{,}5\times0{,}12}C_0=15219{,}62€\)
Podeu reproduir els resultats amb l’Scilab, https://cloud.scilab.in/
Cal remarcar que una de les funcions més importants en Matemàtiques és la funció exponencial, \(\exp x= e^x\). D’aquesta funció i de la seua inversa, la funció logarítmica, parlarem en els propers capítols.
L’Eliana, 22 de març de 2023