
Hi ha coses que romanen gravades a la nostra memòria, sense que hi haja una raó que ho justifique. Això és el que em passa a mi amb el nombre \(\pi\). O, més ben dit, amb el nom del nombre \(\pi\). A l’escola, abans de començar el batxillerat elemental (parle de la prehistòria, quan començàvem el batxillerat als deu anys) féiem servir com a llibre de text únic l’Enciclopedia Grado Medio, de l’editorial Dalmau Carles Pla. Aquell llibre tenia de tot: des de la Historia de España (contada a la franquista manera, per poder passar la censura) fins a la mitologia hebrea, disfressada d’Historia Sagrada, passant per la gramàtica espanyola, les ciències de la natura, la física i la química… i, és clar, les matemàtiques. I fou ací, en la secció de matemàtiques on vaig llegir la frase que se m’ha quedat gravada: per a calcular el perímetre de la circumferència fem servir el nombre que es representa amb la lletra grega \(\pi\) (léase pi). Sí, aquesta ximpleria, «léase pi» és el que se m’ha quedat per sempre a la memòria (bé. Potser no és tan ximple la cosa, atès que era el meu primer contacte amb l’alfabet grec i amb un nombre tan iŀlustre).
Tots ho sabem: la longitud de la circumferència de radi \(r\) és igual al producte \(l=2\pi r\), on \(\pi\), segons aquella enciclopèdia, és un nombre aproximadament igual a \(3{,}1416\). Tots ho sabem, però… sabem per què això és així? Ens ho han demostrat (o, si més no justificat?).
Com que no és gaire difícil, és el que farem tot seguit: calcularem (més o menys, és a dir, aproximadament) la longitud d’una circumferència (tampoc no pretenc ser massa original: això que escriure tot seguit ho podeu trobar fàcilment espigolant per la xarxa; simplement ho faig per divertir-me i intentar divertir-vos).
Començarem amb la típica trampeta de matemàtic: com que no sé quant val el perímetre d’una circumferència, li pose nom:
Definició: El nombre \(\pi\) és el perímetre d’una circumferència de diàmetre igual a \(\mathbf{1}\).
És fantàstic! Com que vull que la longitud de la circumferència siga \(2\pi r\), dic que \(\pi\) és la longitud quan el diàmetre és \(2r=1\). Però bé, resulta que funciona: com ara ja sé qui és \(\pi\), vaig a calcular-lo.
Una primera aproximació (ben basta) pot ser aquesta: agafeu un cilindre, rodegeu-lo amb una corda i mesureu la corda: si ho feu amb una mica de cura trobareu que la circumferència fa una mica més de tres vegades el diàmetre.

Provem de fer alguna cosa una mica més fina: Si dibuixem diversos polígons regulars inscrits en una circumferència de diàmetre igual a \(1\), no ens costarà massa convèncer-nos que, com més gran siga el nombre d’arestes del polígon, més pròxim serà el perímetre d’aquest polígon al de la circumferència.
Així que, elegint un nombre prou gran d’arestes, podem obtenir una aproximació del nombre \(\pi\) tan bona com vulguem. Per tant, hem de calcular la mida de l’aresta d’un polígon regular inscrit en la circumferència.
Hi farem servir una tècnica molt habitual en matemàtiques: un mètode d’aproximacions successives. Anirem doblant el nombre d’arestes per tal d’obtenir aproximacions cada vegada més acurades. I, com que en cada pas doblarem el nombre d’arestes, el que necessitem saber és açò: si ja sabem quant val l’aresta d’un poligon de \(n\) arestes, quina és la mesura de l’aresta d’un polígon de \(2n\) arestes? Potser en Pitàgores ens pot ajudar a esbrinar-ho.
Els gràfics següents mostren el pas de quatre a vuit arestes, però el que farem val per a qualsevol altre cas. Si \(a\) és l’aresta d’un polígon amb \(n\) costats, volem calcular \(b\), l’aresta del polígon amb el doble (\(2n\)) de costats. Com que, a la figura de la dreta, \(BDC\) és un triangle rectangle, pel teorema de Pitàgores, \( b^2 = \left(\frac{a}{2}\right)^2 + (r-c)^2 \). Però això no és suficient per calcular \(b\), perquè no sabem quant val \(r-c\).
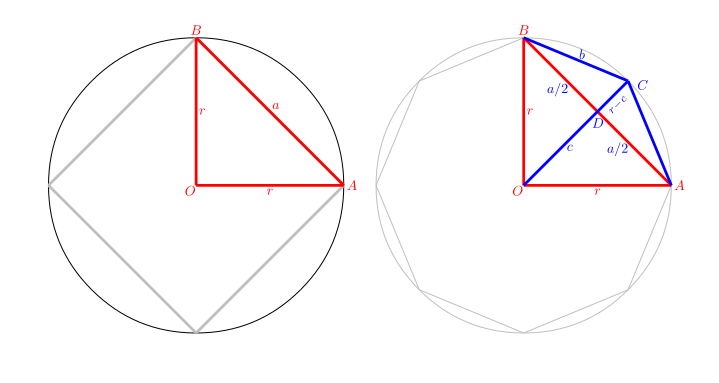
Ara bé, com que \(OBD\) també és un triangle rectangle, \(c^2 + \left(\frac{a}{2}\right)^2 = r^2 \). D’aquesta igualtat podem aïllar \(c\) per a substituir-lo en la igualtat anterior: \(c = \sqrt{r^2-\left(\frac{a}{2}\right)^2} \), així que \[ b^2 = \left(\frac{a}{2}\right)^2 +\left (r-\sqrt{r^2-\left(\frac{a}{2}\right)^2} \right)^2 \]
Si el diametre és \(1\) el radi serà igual a \(1/2\), i tindrem que \begin{equation}b = \sqrt{\left(\frac{a}{2}\right)^2 +\left (\frac12-\sqrt{\left(\frac12\right)^2-\left(\frac{a}{2}\right)^2} \right)^2} = \frac1{\sqrt{2}}\sqrt{1-\sqrt{1 -{a}^2}}\end{equation}
(feu clic ací si voleu veure els càlculs).
Si elegim un primer polígon regular del qual sapiguem calcular la mida de l’aresta, aquesta fórmula ens permetrà calcular successivament les arestes de polígons amb més arestes:
Si \(a_1\) és l’aresta del primer polígon, aquesta fórmula ens dona l’aresta del segon, \(a_2\) i, aquesta, la del tercer, \(a_3\)… D’aquesta manera construïm una successió d’aproximacions successives: a partir d’un valor inicial \(a_1\) podem calcular successivament
\begin{equation}a_{n+1} = \frac1{\sqrt{2}}\sqrt{1-\sqrt{1 -{a_n}^2}}\qquad (1)\end{equation}
La millor elecció, per començar és l’hexàgon, perquè en un hexàgon regular l’aresta és igual al radi, \(a_1=1/2\).
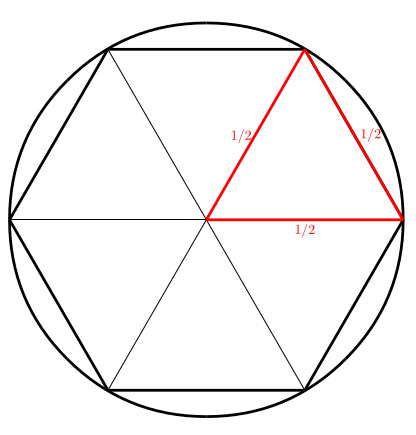
així que el perímetre d’hexàgon és \[P_1=6a_1=6\cdot\frac12=3\]
Si dupliquem el nombre d’arestes la fórmula (1) ens diu que l’aresta del dodecàgon és igual a \begin{equation}a_2 = \frac1{\sqrt{2}}\sqrt{1-\sqrt{1 -a_1^2}} =\frac1{\sqrt{2}}\sqrt{1-\sqrt{1 -\left(\frac12\right)^2}}\approx 0{,}2588190 \end{equation}
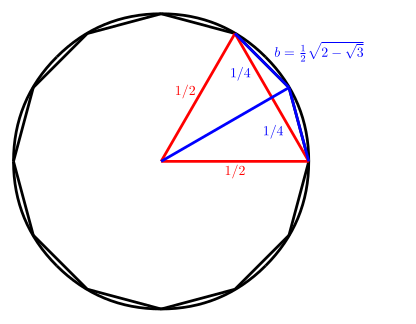
i el perímetre serà \[P_2=12a_2\approx 12\cdot 0{,}2588190 \approx3{,}1058285\]
Tornem a duplicar el nombre d’arestes: ara tindrem un polígon regular de 24 arestes. I la longitud d’aquestes arestes serà igual a \[a_3 = \frac1{\sqrt{2}}\sqrt{1-\sqrt{1 -a_2^2}} \approx \frac1{\sqrt{2}}\sqrt{1-\sqrt{1 -0{,}2588190 ^2}}\approx 0{,}1305262 \]
I el perímetre del 24-àgon és \[P_3=24a_3\approx 24\cdot0{,}1305262\approx3{,}1326281\]
Amb 48 arestes, \begin{equation}a_4 = \frac1{\sqrt{2}}\sqrt{1-\sqrt{1 -a_3^2}}\approx 0{,}0654031 \qquad \mathrm{i}\qquad P_4=48a_4\approx3{,}1393502\end{equation}
Amb 96 arestes, \begin{equation}a_5 = \frac1{\sqrt{2}}\sqrt{1-\sqrt{1 -a_4^2}}\approx 0{,}0327191 \qquad \mathrm{i}\qquad P_5=96a_5\approx3{,}1410320\end{equation}
Aquesta expressió aproxima \(\pi\) amb tres decimals exactes.
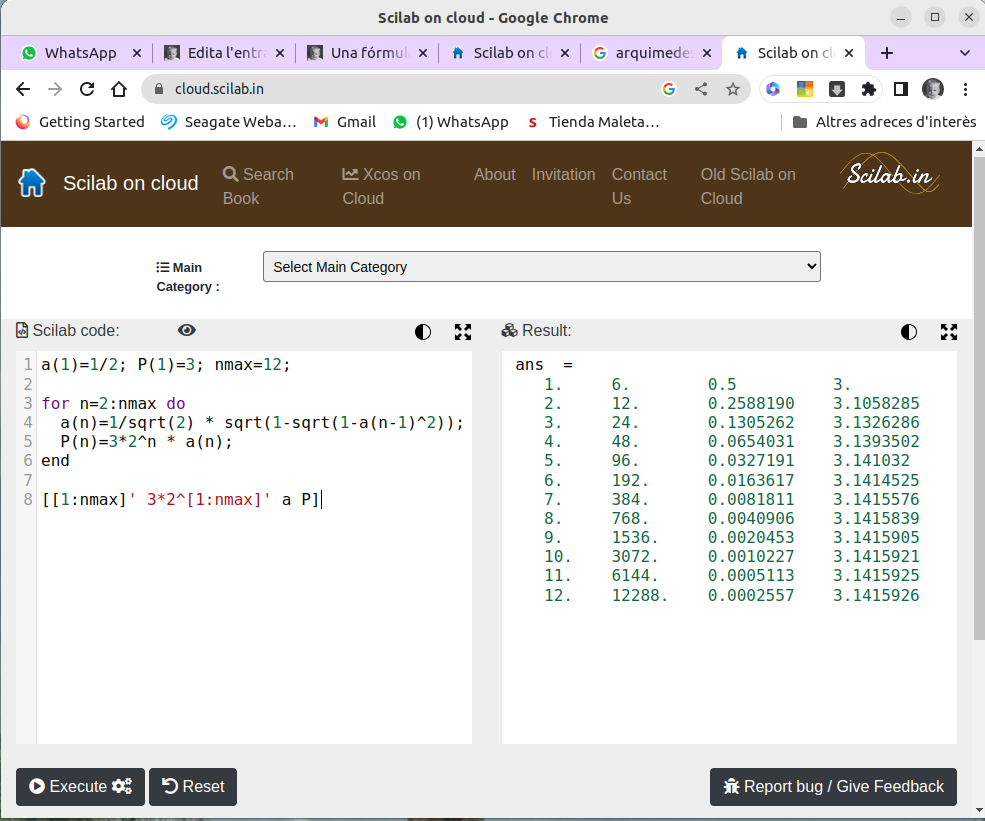
Els càlculs que hem anat fent podeu reproduir-los fàcilment amb qualsevol calculadora científica que instaŀleu a la vostra tauleta (o al vostre mòbil).
Jo els he fet amb la versió en línia del sistema de càlcul científic Scilab, que podeu executar des d’aquest enllaç:
(Si us sona el MATLAB, l’Scilab n’és el cosí germà gratuït)
La imatge adjunta mostra els resultats que s’obtenen amb l’Scilab en les 12 primeres iteracions.
La darrera iteració (amb \(6\times 2^{11}=12288\) arestes) és exacta en totes les xifres que s’hi mostren (la millor aproximació que podem obtenir amb aquesta versió de l’Scilab és \(\pi\approx 3{,}141592645\), perquè a partir d’aquí els errors d’arrodoniment són més grans que l’error).
Arquimedes feu servir un mètode molt semblant a aquest per a aproximar el nombre \(\pi\). Però ell no tenia calculadora ni feia servir l’algorisme de l’arrel quadrada que coneixem nosaltres! En comptes d’això, aproximava les arrels mitjançant nombres racionals (fraccions). Nosaltres hem construït una successió creixent d’aproximacions de \(\pi\) per defecte, perquè els polígons inscrits a la circumferència sempre tenen un perímetre més menut que la circumferència. Arquimedes feia servir també aproximacions per excès, amb els polígons circumscrits.

Amb aquest procediment, arribà fins al polígon de 96 arestes i obtingué
\begin{align*}&&\frac{223}{71} &< \pi <\frac{22}{7}\\\text{és a dir}\\&&3{,}1408451 &<\pi<3{,}1428571\end{align*}
Si aproximem \(\pi\) per la mitjana tindrem
\[\pi\approx \frac{\frac{223}{71} +\frac{22}{7}}{2}\approx 3{,}14185\]
que no està gens malament! Per cert, ja hi tornarem, però l’autèntic dia de \(\pi\) no és el 14 de març, sinó el 22 de juliol: \(22/7\).
Els deures
Exercici 1: Aproximeu el nombre \(\pi\) fent servir polígons de 4, 8, 16… arestes.
Exercici 2: Aproximeu el nombre \(\pi\) mitjançant polígons circumscrits de 6, 12, 24… arestes.
Exercici 3: Sabem que la longitud de la circumferència de radi igual a \(1/2\) és igual a \(\pi\). Però, perquè la longitud de la circumferència de radi igual a \(r\) és \(2\pi r\)?
Exercici 4: Demostreu que l’àrea del cercle de radi igual a \(1/2\) és igual a \(\frac{\pi}{4}\).
(suggeriment: en la fórmula \(c = \sqrt{r^2-\left(\frac{a}{2}\right)^2} \), que hem vist adés, \(a\) i \(c\) són l’aresta i l’apotema del polígon)
Exercici 5: Demostreu que l’àrea del cercle de radi igual a \(r\) és igual a \(\pi r^2\).
Fi de festa
Si encara us queden ganes de llegir, de propina, obtindrem una altra fórmula espectacular: aplicant la fórmula (1) hem trobat \begin{equation}a_2 = \frac1{\sqrt{2}}\sqrt{1-\sqrt{1 -a_1^2}} =\frac1{\sqrt{2}}\sqrt{1-\sqrt{1 -\left(\frac12\right)^2}}\end{equation}
Doncs bé, aquesta expressió es pot simplificar fàcilment: \begin{equation}a_2 = \frac1{\sqrt{2}}\sqrt{1-\sqrt{1 -\left(\frac12\right)^2}} =\frac1{\sqrt{2}}\sqrt{1-\sqrt{\frac44 -\frac14}}=\frac1{\sqrt{2}}\sqrt{1-\frac12\sqrt{3}}=\frac12\sqrt{2-\sqrt{3}}\end{equation}
Fent manipulacions semblants, la següent iteració també es pot simplificar \begin{equation}a_3 = \frac1{\sqrt{2}}\sqrt{1-\sqrt{1 -a_2^2}} =\frac1{\sqrt{2}}\sqrt{1-\sqrt{1 -\left(\frac12\sqrt{2-\sqrt{3}} \right)^2}} = \frac12\sqrt{2-\sqrt{2+\sqrt{3}}} \end{equation}
I, successivament,
\begin{equation}a_4 = \frac12\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{3}}}} \qquad a_5 =\frac12\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}}}\qquad a_6 =\frac12\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}}}} \end{equation}
De manera general, es pot demostrar (pel mètode d’inducció, si sabeu què és això) que, a partir de \(n=2\),\begin{equation}a_n = \frac12\underbrace{\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+\dots+\sqrt{3}}}}}}_{n \text{ arrels quadrades}} \end{equation}
En conseqüència, el perímetre del polígon de \(3\cdot 2^n\) arestes és
\[P_n = 3\cdot 2^n \frac12\underbrace{\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+\dots+\sqrt{3}}}}}}_{n \text{ arrels quadrades}} \]
Quan \(n\) es fa infinit els perímetres es converteixen en \(\pi\). Això és el que els matemàtics anomenem límit, així que
\[ \pi = \lim_{n\rightarrow\infty} 3\cdot 2^n \frac12\underbrace{\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+\dots+\sqrt{3}}}}}}_{n \text{ arrels quadrades}} \]
L’Eliana, 16 de febrer de 2023